【注】本文转载自http://blog.csdn.net/adminabcd/article/details/46672759,仅作备份以备参考。
分析过程:
(1)先考虑只有一个节点的情形,设此时的形态有f(1)种,那么很明显f(1)=1
(2)如果有两个节点呢?我们很自然想到,应该在f(1)的基础上考虑递推关系。那么,如果固定一个节点后,左右子树的分布情况为1=1+0=0+1,故有f(2) = f(1) + f(1)
(3)如果有三个节点,(我们需要考虑固定两个节点的情况么?当然不,因为当节点数量大于等于2时,无论你如何固定,其形态必然有多种)我们考虑固定一个节点,即根节点。好的,按照这个思路,还剩2个节点,那么左右子树的分布情况为2=2+0=1+1=0+2。
所以有3个节点时,递归形式为f(3)=f(2) + f(1)*f(1) + f(2)。(注意这里的乘法,因为左右子树一起组成整棵树,根据排列组合里面的乘法原理即可得出)
(4)那么有n个节点呢?我们固定一个节点,那么左右子树的分布情况为n-1=n-1 + 0 = n-2 + 1 = … = 1 + n-2 = 0 + n-1。此时递归表达式为f(n) = f(n-1) + f(n-2)f(1) + f(n-3)f(2) + … + f(1)f(n-2) + f(n-1)
接下来我们定义没有节点的情况,此时也只有一种情况,即f(0)=1
那么则有:
f(0)=1,f(1)=1
f(2)=f(1)f(0)+f(0)f(1)
f(3)=f(2)f(0)+f(1)f(1)+f(0)f(2)
.
.
.
.
f(n)=f(n-1)f(0)+f(n-2)f(1)+……….+f(1)f(n-2)+f(0)f(n-1)
该数列称为卡特兰数(Catalan数),该递推关系的解为:
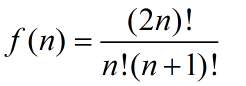
即含n个节点的二叉树有f(n)种形态.
离散数学笔记:一个高度为n的二叉树至少有n + 1个节点,至多有2^(n+1)-1个节点。
 MikuAlpha's Blog
MikuAlpha's Blog